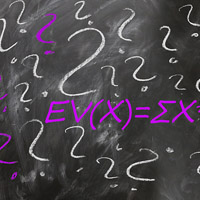What is Expected value?
The Expected value (EV) is a term used in statistics. We also refer to it when analysing probability. It is used in situations such as finding a probability of investments, betting, poker or generally in gambling. The principle of calculating EV is based on evaluating all scenarios, outcomes and probabilities of each outcome. The result of the analysis is presented as a positive or negative value that helps investors determine what level of risk to take with each action and choose the most optimal scenario.
The formula of expected value
To calculate EV, you should identify each scenario that may occur and the probability of its occurrence. The EV is the sum of all net values of each scenario multiplied by their individual probabilities. There is a very simple formula to use:
EV(X)=∑X*P(X)
To better understand the Greek symbol in the first formula you can of course use the following itemized formula:
EV = x1*p1 + x2*p2 + … + xN*pN
- 1) x = the net value for each (1 through N) outcomes.
- 2) p = the probability for each (1 through N) outcomes.
Example #1: Lottery game with NEGATIVE Expected value
Suppose a lottery is giving an outcome of a grand prize of $500 and two consolation prizes of $100 each. Altogether there was 100 tickets sold at $10 each at total amount of $1000. So the next step to calculate EV is to calculate first the net value for each outcome and a probability of occurance of each outcome:
- 1) One grand prize of $500 minus the ticket price $10 = $490 net value and the chance to win is 1/100.
- 2) Two runner up prizes of $100 each minus the ticket price $10 = $90 net value and the chance to win is 2/100.
- 3) If you haven‘t won anything, then your net value is -$10 and the chance to lose is 97/100.
What is the expected value in this lottery game example? Let's put the numbers into formulas above:
- EV = (490*1/100) + (90*2/100) + (-10*97/100)
- EV = 4.90 + 1.8 + (-9.7)
- EV = -3
The obtained value of EV is -3 and this result can be interpreted in many ways, but the key for us is the situation for which the computation was generated. The lottery game has a negative EV (= -3) which we interpret that: for every ticket of $10 you can expect a loss of $3.
How can you make a loss of $3 when rules of lottery game do not allow such behaviour? Because the expected value is actually the expectation; mathematical expectation, average, mean value etc. so you should ponder EV as an average result of many game attempts. That means, if you play this lottery game multiple times, you can expect the average loss of $3 pet ticket. So, looking at this rationally you probably should not play this game.
Example #2: Lottery game with POSITIVE Expected value
A lottery is giving a grand prize of $500 and two second prizes of $200 each and three consolation prizes of $50 each. There were again 100 tickets sold at $10 each at a total amount of $1000. So, next step again is to indentify all results of this game with the net income for each scenario as in previous example:
- 1) One grand prize of $500 minus the ticket price $10 = $490 net value and the chance to win is 1/100.
- 2) Two consolation prizes of $200 each minus the ticket price $10 = $190 net value and the chance to win is 2/100.
- 3) Three consolation prizes of $50 each minus the ticket price $10 = $40 net value and the chance to win is 2/100.
- 4) If you don't win anything, then your net value is -$10 and the chance to lose is 94/100.
What is the expected value in this lottery game example? Let's put the the numbers into formulas again:
- EV = (490*1/100) + (190*2/100) + (40*3/100) + (-10*94/100)
- EV = 4.90 + 3.8 + 1.2 + (-9.4)
- EV = 0.5
Based on given explanation in the previous example we can evaluate this EV of 0.5 very positively and and find that the example in second scenario is quite attractive game. Basically we can expect a profit $0.5 from each ticket of $10.
Although average profit of $0.5 per ticket doesn’t look like hitting the jackpot, the positive EV makes this game look good. Especially if we move the game to the extreme: if we buy all tickets of $1000 the lottery payout would total to $1050 (sum of all prizes). That is more than price of all tickets! On the other hand if you did the same in the previous example and bought all tickets of $1000 the lottery would actually pay back to you only $700. As unfair as it may seem, this is standard principle of every lottery or gamble.
Example #3: EV in Binary Options vs. Roulette in casino
Following section of this article explains the same principle of EV however this time using Binary Options. As this article was originally written as a part of this article [link] the principle of following examples will repeat the ones already given. That means if you have read and understood examples #1 and #2 above you can easily skip this section.
Negative Expected value of binary options
If you are betting in binary option you have practically just two possible outcomes of the game. And you know them before you place your order: either win or lose. This makes the calculation of EV very simple.
Lets use a basic example of betting $10 with return 90% of deposit. Why do we use this extreme example? Return 90% is pretty high, and brokers rather offer returns lower then 80%, so lets make this more attractive. And $10 is very small amount that many brokers happily advice that it is safe to use as it a “safe small bet”. This is to demonstrate a big advantage that you can bet very small amounts. So, here is the calculation:
- 1) Win situation: If you bet $10 with 90% return, you can win $9 (off course you will get back your deposit of $10). And chance to win is 50% = 50/100
- 2) Lose situation: If you lose you will lose everything you bet (your full deposit of $10). The risk of loss is also 50% = 50/100
Let's put the the numbers into formulas again:
- EV = (9*50/100) + (-10*50/100)
- EV = 4.5 + (-5)
- EV = -0.5
As you can see even such atractive offer as it is visible in our example has a negative Expected Value. If you want to avoid any unpleasant loss when trading binary options, you should look at value -0.5 from a binary options broker's point of view. And because of EV can be also interpreted as the average value we should interpret this value as: the binary options brokers have profit of $0.5 from every $10 bet that trader closes.
Expected value and Roulette in casino
The roulette is a demonstratively named and compared to binary options because the chance to win is there based on the pure luck – to put it simply it is 50:50. But actually the chance to win is lower then 50%! In fact, roulette has 18 black and 18 red slots and 2 green slots that means the real odds of winning is 47.4% if you wager on black or red. And casino has 52.6% chance to take your money.
For calculation of expected value in roulette lets use example of betting $10 on black:
- 1) 1 of 18 black slots: you are right and you can win $20 ($10 deposit and $10 your reward). And chance to win is 47.4 % (18/38)
- 2) 1 of 18 red slots: you are wrong and you will lose the whole bet of $10. The risk to lose is also 47.4% because there is equal amount of slots (18/38)
- 3) 1 of 2 green slots: you are wrong again and you will lose the whole bet of $10. The risk to lose is however also 5.2% (2/38)
Let's fill the the numbers into formulas:
- EV = (10*18/38) + (-10*18/38)+ (-10*2/38)
- EV = 4.74 + (-4.74) + (-0.53)
- EV = -0.53
As you can see the casino is really business for generating money. Even though you think your chances to win are 50:50, just two green slots guarantee the casino's average profit of $0.53 per game, in another words, your average loss of $0.53.